HEEDS

HEEDSは自己学習型の探査アルゴリズムを持つ最適化ツールです。
通常、単独で使用することはありません。解析ツールなどと併用することで適した出力値となるよう入力値を操作します。
例えば、軽量化であれば [寸法変更]→[解析]→[強度評価]→[寸法変更]…
これを自動で行います。評価する入力変数や出力項目が複数ある場合には果てしなく大変な作業になりますが、HEEDSのSHERPAアルゴリズムで、最適解により早く近づくことができます。繰り返し作業の自動化と可視化による気付きで、新たな発見と可能性に大きく貢献します。

HEEDS ４つの特徴

HEEDS01

① 探査アルゴリズム ～SHERPA～

最適解にいかに早くたどり着くかは重要です。HEEDSの探査アルゴリズムSHERPAは臨機応変です。様々な探査手法を同時に使用します。探査範囲も全体と局所を同時に行い最善の方法を選択します。
未知の山脈の頂上を目指すときに必要なのは、すべてのクライミング戦略を知っており、遭遇する地形・気象に合わせてアプローチを調整できるSHERPAです。
HEEDS には、複数の探査アルゴリズムを組み合わせて重み付けし、必要に応じて戦略を変更・調整する SHERPA フレームワークが含まれています。SHERPAフレームワークはハイブリッドな適応性があり、新しい探査アルゴリズムが開発された場合にも、それをSHERPAフレームワークに追加するだけで、他のアルゴリズムと組み合わせてその利点を活かすことができます。

HEEDS02

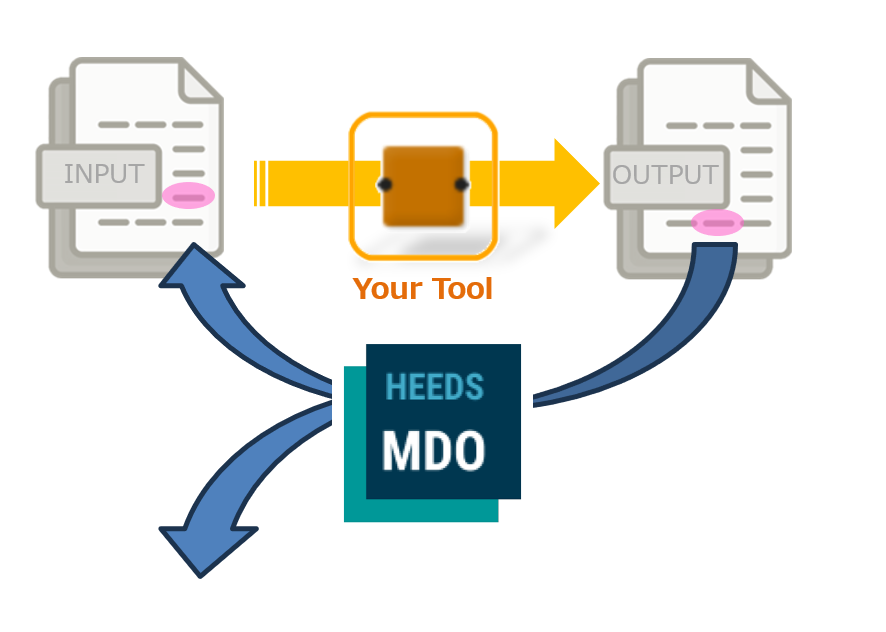
② 汎用ツールとの連携

HEEDSによる最適化を行うために必要なものは、解析ツールなどの計算プログラムとその入出力データです。HEEDSは出力データ中の結果値を探査アルゴリズムで評価し入力変数を求めます。求めた入力変数を入力データに反映してしてソルバーに返します。入出力データ中のどの項目をHEEDSが使用するのかを設定する作業をタグ付けといいます。
解析ツールによって入出力の書式が違いますが、HEEDSではタグ付けなどの設定が簡便にできるよう様々なツールに対してポータルを用意しています。
ポータルが無い場合でも、入出力データがテキスト形式であればタグ付けは簡単にできます (バイナリー形式の場合には、APIで対応することになります)。
ポータルは今後も必要に応じて拡充される予定です。

HEEDS03

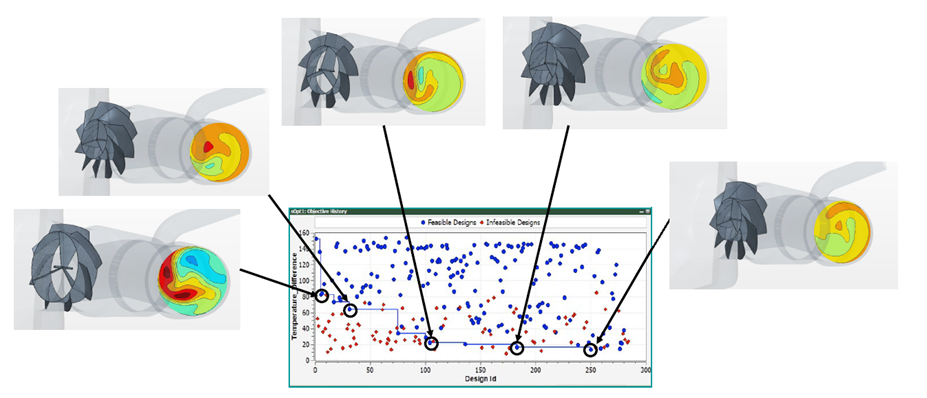
③ 多彩な出力プロット

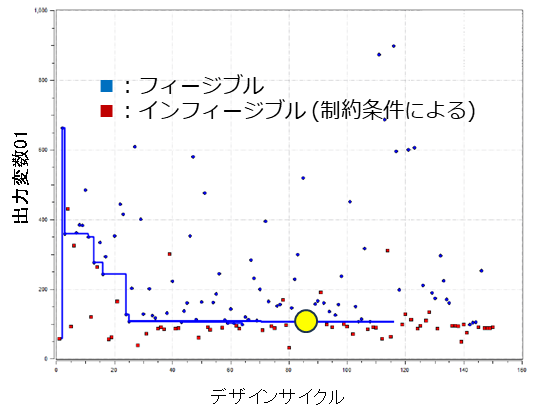
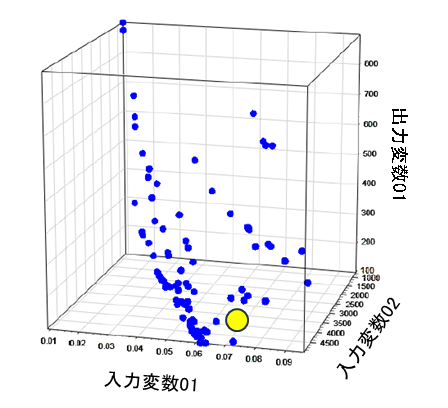
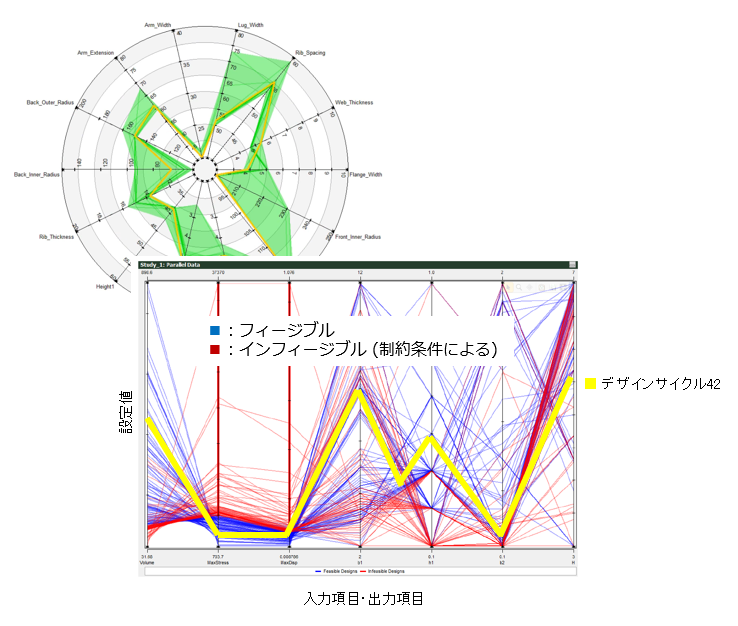
履歴	スタディが進むにつれて入力変数または出力変数がどのように変化したかを示します。
2D・3Dプロット	入力変数または出力変数を、デザインセット内のその他の変数に対してプロットします。
パラレル プロット	複数の入力変数と出力変数間の関係を、グラフィック表示します。
デザイン テーブル	デザインデータを表形式で作成します。
確率分布	パラメータの値の確率分布をヒストグラムで表します。
累積確率分布	パラメータ値の履歴を累積確率分布で表します。
モデルビュー	スタディにおけるデザイン形状を表します。
カーブフィット	選択したデザインがターゲットにどれだけ近いかをカーブで可視化。
相関図	選択したデータのピアソンの相関係数を表します。
自己組織化 マップ	データ内のパターンと関係をクラスタリングします。
ヒートマップ	入出力パラメータ値を色付きセルのマトリックスで表します。
制約の逸脱	探査中に逸脱した制約条件とその度合いを識別します。
パレート フロント	パレート最適化スタディの出力を競合する出力に対してプロットします。
応答曲面	応答面を 入力変数の関数として表示します。
応答曲面誤差	出力変数評価で最も適合した誤差モデルを識別するときに役立ちます。
寄与率	出力変数に対する入力変数の寄与率の大きさをパーセントで比較するパレート図です。
因子の影響度	入力変数が 出力変数に与える影響度を線形のグラフで表します。
因子の相互作用	出力変数に対して 入力変数が持つ交互作用を線形のグラフで表します。
ユーザ定義	ユーザーによって生成されたデータを表示します。

HEEDS04

④ 新たな評価と気付き

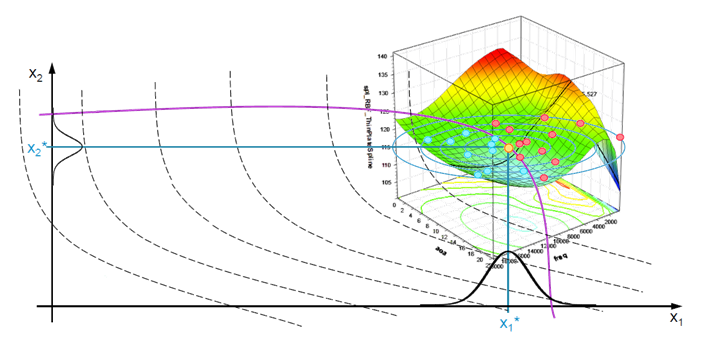
HEEDSには、設計空間の特徴を評価するためのポスト処理が用意されています。
設計空間とは、入力変数と出力変数の関係を空間上に図示したものです(1度に図示できるのは3次元までです)。設計空間の傾向を理解することで更なる改善や気づきを得ることができます。
また、出力が競合関係にあるようなケースでは最適解は1つに求まりません。各変数のトレードオフの限界(パレートフロント)を効率的に探査し、新たな発見と可能性に大きく貢献します。
更に、入力変数に確率密度関数を用いることができますので、製造公差に対する信頼性評価としての活用も期待できます。