Simcenter 3D 音響解析

Simcenter 3DではRay Acoustics(音線法)、FEM(有限要素法)と BEM(境界要素法) に対応しています。

Ray Acoustics (音線法)

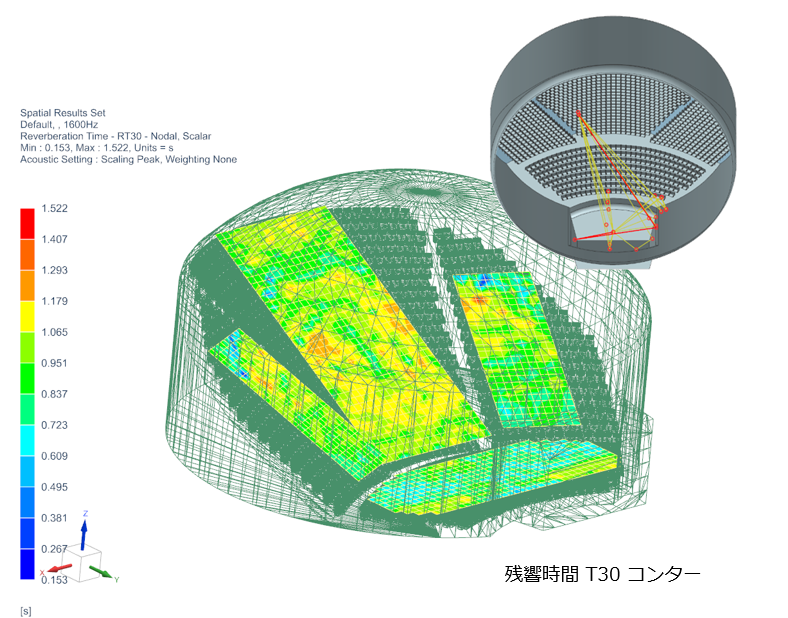
数値解析の主流である 有限要素法(FEM)や境界要素法(BEM)では空気層の音場が離散的に計算され、周波数毎の音圧レベルや回折の様子を音圧コンター図で確認することができます。この計算には多くの計算点が必要で、解析時間がかかってしまうのが解析者の悩みの種です。

Ray Acousticsでは高周波数領域における問題を近似的に求めます。高周波では、音波は光線のように伝搬すると考えることができます。Ray Acoustics solutionでは各音源から受音されるまで、光線がどこを伝搬するのかをジオメトリ形状的に算出します。このステップは周波数に依存しません。FEMやBEMと違い、Ray Acoustics は流体領域の離散的ファクターに依存せず、ジオメトリ形状の空間位相にのみ依存します。このことは、Ray Acousticsが高周波で大きなモデルに適応できるキーポイントになります。ひとたびレイパスが算出されると、空気の材料特性を使って各周波数における音の伝達が求められます。

音響指標と聴覚化

音線法は周波数応答結果からインパルス応答を作成します。計算コストが小さいため、周波数ステップの小さい解析が可能となります。このことは、インバースDFTで得られるインパルス応答時間が長いことを意味します(例えば、2秒間の時間ドメインを得るためには0.5[Hz]刻みの解析が必要です)。インパルス応答結果を利用して、伝達特性下におけるオーディオ信号音を再現します(聴覚化)。音の広がりや残響といった音響品質評価を強力にサポートします。

FEMとの連携

形状の複雑な障害物よる音の回折現象を表現するのはFEMやBEMが適切ですが、回折後の音響伝搬については音線法が適している場合があります。例えば、パーキングセンサーやカーステレオなどは音源近傍の形状が音の指向性に影響するが、評価する放射音空間が広域の場合です。このようなケースでは、まず音源近傍をFEMで解析して境界面における音圧分布を求めます。それを指向性を持った音源に変換し、Ray Acousticsで用います。

FEM (有限要素法)

Simcenter NastranソルバによるFEM解法をサポートしています。FEMはBEMに比べて解析速度が速いのが特徴ですが、音響領域をモデリングする必要があり、規模が大きくなりがちです。
Simcenter 3Dでは以下のような機能でFEM音響をサポートしています。

流体領域モデリング

FEMAO (FEM Adaptive Order)

要素次数を上げることで同一メッシュのまま解析の周波数レンジを上げることができます。各要素内の圧力場を表現するために、形状関数と自由度の数を増やします。FEMAOは要素ごとおよび周波数ごとに次数を調整するため、圧力場をより効率的に表現できます。

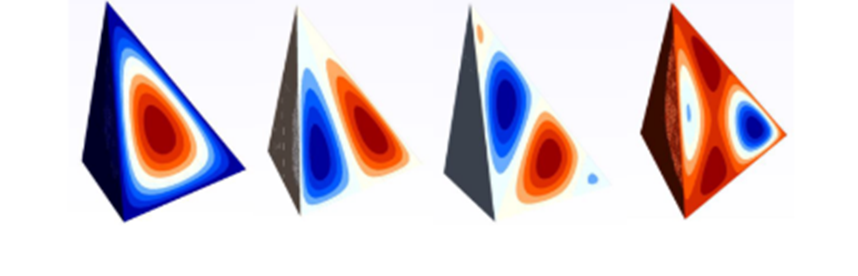
自動一致レイヤ (AML)

無限外部音響モデリング(非反射境界条件)を容易にしました。ALM法は、周波数や入射角に関係なく外向きの波を吸収するレイヤとして流体メッシュの外表面に設定します。

更に、流体メッシュの有無にかかわらず、マイクロフォンメッシュを作成した任意の位置における音響結果を出力できます。AML境界の内側では流体節点からマイクロフォンの位置に結果を補間します。流体メッシュの存在しないAML境界の外側では、AML境界上の圧力・速度を境界積分して算出します。

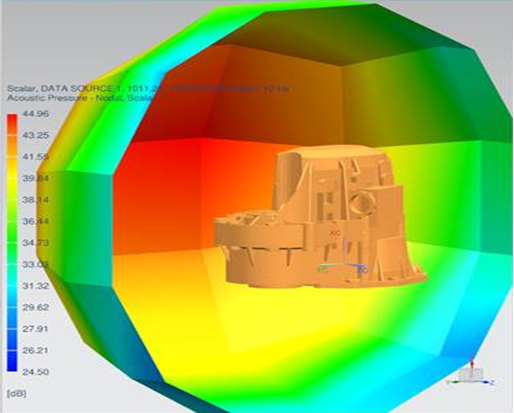
音響伝達ベクトル (ATV)

振動に対するマイクロフォン位置での音響応答を効率的に計算することができます。ATVは流体ボリュームにおける周波数依存音響ベクトルで、マイクロフォン境界の振動面における単位体積速度当たりの圧力として算出されます。このATVを利用することで、構造振動から音響圧力への弱連成が容易になり、エンジンやモータ、ギアボックスなど複数の回転状態をもつモデルの繰り返し解析のスループットを上げることができます。

BEM (境界要素法)

BEMは、音響領域そのものではなく、音響領域の境界を使用して音響量を解析します。境界表面メッシュ以外は不要になるため、外部放射音のシミュレーションを簡素化できますが、システムマトリックスはFEMより密になります。
Simcenter 3DではH -MatrixやFast Multipoleといった手法で高周波数域における計算負荷を低減し高速化を実現しています。また、BEMではモーダル法による強連成解析が可能です。構造に対して音響圧力の影響を無視できないような場合に使用できます（例えばスピーカーのデザイン等）。