- テーマ:空力騒音
- キーワード:気流音、空力騒音、流体騒音、騒音、音響、乱流、圧縮性
背景
風や空気の流れにおいて生じる圧力変動が音波として周囲に伝搬することで音が発生し騒音源となることがあります。
この流れからの音は、列車や自動車及び航空機等の輸送機械、医療機器、情報機器や家電製品、空調や換気設備、建築構造物などに広く関係し騒音問題となるため製品の開発に際して対応が求められています。
例えば、太鼓などをたたくと音が発生しますが、これは太鼓の膜が振動することによって周囲の空気中を波が伝搬する振動音がですが流れからも音が発生します。
よく風が強いときに電線がヒューと鳴る音は、流れが電線を通過する際に生じる渦の速度変化が音源となるもので、この空気の流れから発生する音を「空力騒音」と呼んでいます。
空力騒音が問題となる流れ場は、一般にレイノルズ数が高く、物体形状も複雑なこともあり、圧縮性を考慮した流れ計算の密度変化から変動音を直接計算する方法ではなく、音響アナロジーを利用した分離解法が使われることが多くあります。
音響アナロジーによる手法のうちProundmanは、Lighthillの音響アナロジーを用いて、平均流がない等方乱流によって生成された音響パワーの式を導き出し、LilleyはProudmanの元の導出では無視された時間遅れを考慮した式を導出しました。
双方の導出では等方乱流の単位体積(W/m3)により以下の式のように音響パワーを予測します。
音響パワー (W/m3):
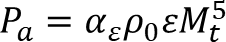
ここで、
モデル定数: αε=0.1
(SarkarおよびHussainiのキャリブレーションに基づく)
流体の密度 (kg/m3): ρ0
乱れの散逸率 (m2/s3): ε
乱流マッハ数: Mt
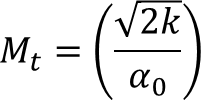
ここで、
乱れのエネルギー (m2/s2): k
流体の音速 (m/s): α0
Proudmanによる広帯域騒音源モデルは、乱流の運動エネルギー(k)と散逸率(ε)から、低マッハ数の等方性乱流における単位体積あたりの音響パワーの局所的な寄与の近似値を示すことができ、過渡的な解を必要としませんので高速に音源を把握することが出来ます。
概要
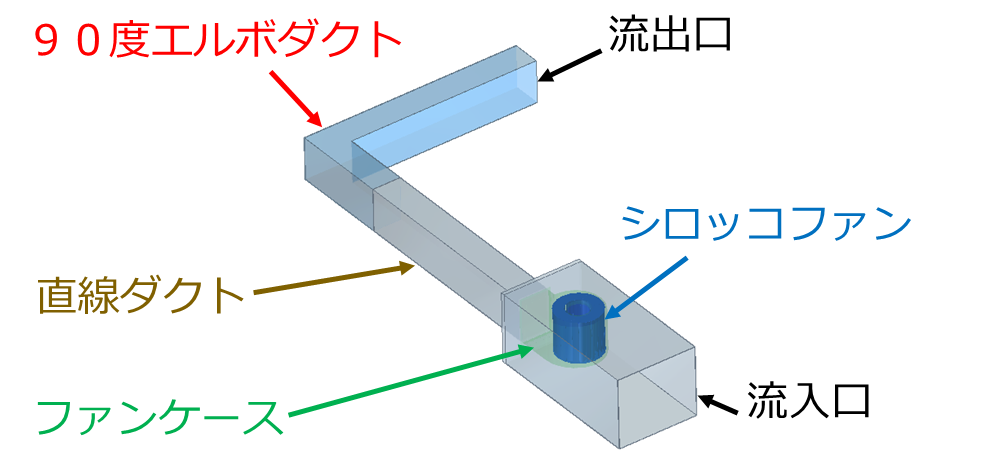
- この事例では、シロッコファンによって送風された気流が角型ダクトを流れており、
ファンから3000㎜下流に90度の角度で折れ曲がって流出します。
このモデルに対しProudmanによる音響アナロジーを用いて90度の曲がり部の曲率を以下の図のように3種類変化させた場合の音響パワーを比較しています。
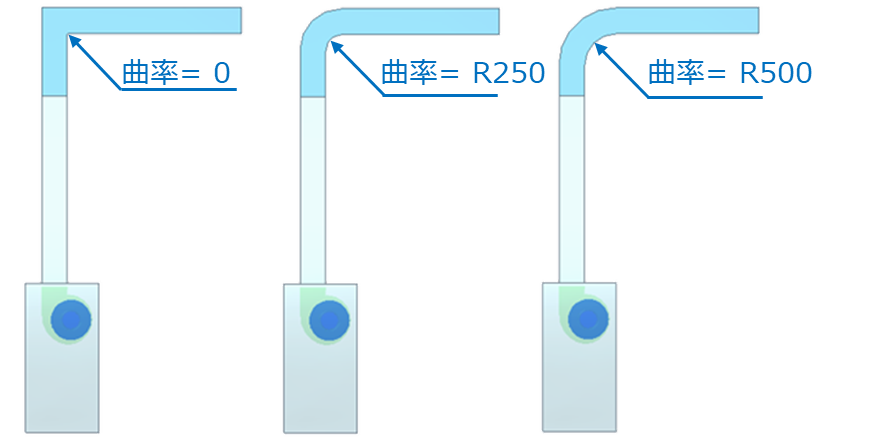
| 項目 | 値 |
|---|---|
| 流体 | 空気 |
| 温度 | 20.0℃ |
| 粘性係数 | 1.822×10-5 Pa*s |
| 密度 | 1.205 kg/m3 |
| 流入 | 質量流量: 3.72 kg/s |
| 流出 | 101325 Pa |
| シロッコファン回転数 | 300 rad/s |
- 3種類のダクト形状について音響パワーレベル(dB)の分布及び特定点での値を以下に示します。
曲率 = 0の場合、エルボから下流で50dB程度のレベルが広く存在していますが、曲率 = R250では30dB程度まで下がり、曲率 = R500では20dB程度になることが分かります。
ダクト曲がり部から発生する空力騒音については、曲率や整流版などによる整流が有効であることが分かります。
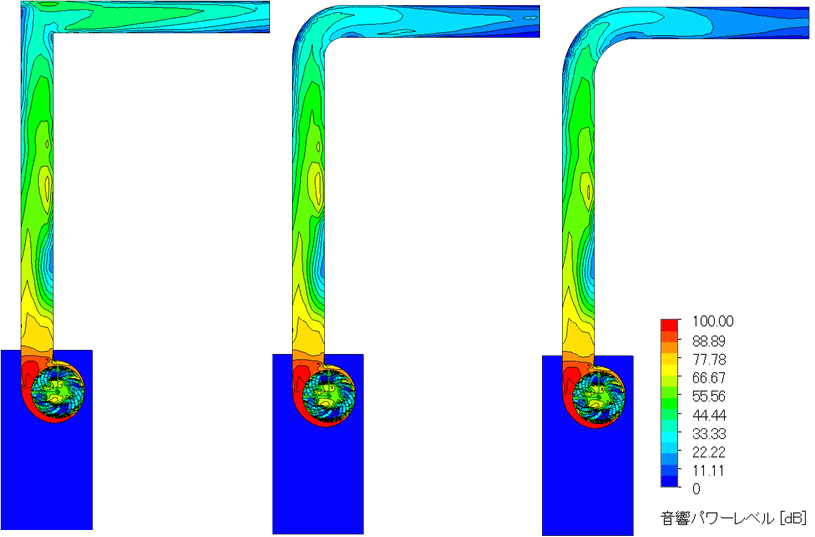
| 曲率 = 0 | 曲率 = R250 | 曲率 = R500 | |
|---|---|---|---|
| 音響パワーレベル (dB) | 38.51 | 24.08 | 18.14 |
 RCCM-STRUCT
RCCM-STRUCT